The Startup

The Startup

We Cannot Wait On this:
 
“Somebody will build it; and when it's built, it will work; and when it works people will begin to use it, and it will begin to displace all other forms of energy.” – Robert Bussard

     My friend is an entrepreneur. He argued all someone needed to do is show scientifically that the polywell can work and there will be a flood of money into the technology. He said: “if you can prove to a VC that this will work, that we need X amount of dollars to get there first - then money will be spent; because that is a great bet.” Right now, businesses are looking for new ideas. Many companies have accumulated stores of cash during this recession; through stock buybacks and prudent spending. I would argue the environment is ripe this technology to flourish – that is, if it works.

     If we had a machine built, today, here is what we would try. Run the reactor with lots of low velocity electrons, tightly held together, with a few high velocity ions injected. Give the electrons ample space for highly efficient recirculation. Try and reflect back the X-rays. Try to get the DD or DT ions above 10 KeV. See if a resonance condition exists, if not try and pulse the machine or try and tune it. There is no guarantee this strategy will work; so adjust as needed. Use dimensionless numbers everywhere you can to simplify operations. Standardize reactor design, the simpler and more uniform and interchangeable the parts, the better. Focus on getting a working machine – even if it is inefficient - or poorly characterized – and churn out products.

    If this machine worked, it has the clear potential to re-launch the American economy. Given that it could be a green energy source, it also has the ability to put America back on moral footing with the rest of the world. Beyond the positives, there is a darker side to consider. If another nation was able to get this working first, it could be disastrous for the United States. A hostile military force, removed from its dependence of oil, could simply cut oil supplies to the US and not care. That is the nightmare scenario. Frankly, America cannot wait on this technology.

Iran and The Polywell: 

    Many groups are not waiting. On October 12th 2011, the atomic energy organization of Iran published a basic polywell paper in the Physics of Plasma Journal. The work lays out the rudiments of the reactor and simulates it under two operating modes; using common plasma simulation software. The software is based on particle in cell (PIC) plasma software [8]. The geometry simulated in the paper is very unclear, but based on the description provided we were able to draw the diagram below.



 The geometry they simulated was less like six rings and more like six truncated cones. They only simulated a two dimensional plane out of the reactor – one would assume you could extrapolate the 3D behavior from this 2D plane. They simulated the rings by creating eight “wires” flowing current into and out of the plane. The details of ion and electron guns, as well as the biasing voltage, are included in the figure above. We do not agree with this geometry. There is too much metal in the center of the reactor, causing conduction losses. The electrons need high recirculation inside the reactor; Rider, Bussard and Ligon all mention this. The rings should look more like hula hoops and less like hubcaps – with ample space to allow the electrons efficient recirculation. Plus, the rings should be insulated and held at a uniform voltage to further cut down on conduction losses. This work was very similar to work presented by Dr. Joel Roger, in 2009 at an IEC workshop. Joel simulated two vacuum chambers, one 70 centimeters, square and one 140 centimeters, square, the same size as the chamber simulated here. Joel simulated the rings at 25,000 and 50,000 volts, compared with the 150,000 volts used in this work [4, 5].

      The paper simulated the ion guns inside the rings – so that all the ions are pushed into the center [5]. The ions must be injected into the well at a certain energy so that they can fuse, but not so much that they escape the well. Ligon mentioned this before; and this probably means the final reactor will have to tune its’ ion guns. As far as we know, there is not a requirement that the guns be inside the magnetic field. The paper simulates two modes of operation: one where the rings generate low magnetic field strength and one where the rings generate high (10 times) magnetic field strength. The magnetic fields are turned on and kept constant throughout the simulation - which simulates a pulse of time up to 14 microseconds. During this time, the electron and ion guns are turned on, filling the magnetic field “cup” with ions and electrons. A chart of the magnetic fields used and the results obtained for each run is included below.




What The Iran Work Is Lacking:

    There are many problems with this Iranian paper. For one, the simulation itself is no substitute for real data. The work did not include any comparison to analytical solutions for the magnetic field – either the field made by the rings or the field made by the electron cloud. It did not attempt to connect confinement to the underlining concept of a magnetic mirror. The work was also weak because it limited itself. By focusing on confinement alone, the work sidestepped the issues of fusion rates, thermalization, the virtual anode and x-ray cooling. Simply put, the work was very poor. We were surprised it got published in the physics of plasma – a highly respected, world renowned journal for fusion research. The University of Sydney December 2011 paper, from the same journal, is much more exciting [6].

     This Iranian work piggy backs off of an earlier paper published physics of plasmas in June of 2011 [7]. That work did not get nearly as much attention, because it reported on classical inertial electrostatic fusion, technology that is decades old. But, there is an important message here. One we should pay attention too. The message is this: the Iranians are attempting to start a polywell fusion program [9]. This is no big deal, right? America does care if its sworn enemy has this technology. That is not reckless, is it?

University of Sydney and the Polywell: 

    The Iranians were not the only group to publish polywell work this Fall; Joe Khachans group at the University of Sydney also published a paper online on November 3rd 2011 [6]. In December, the paper was the 8th highest downloaded paper on the Physics of Plasma site. The paper looks to be very significant. It discusses a coherent picture of confinement inside the machine, using theory and simulation work to back up claims. This blog hopes to write an entirely separate post, explaining the work for the lay audience. We plan to treat the work with as high a level of skepticism as we have other work.

     Where is the Navy, in all of this? The folks at talk-polywell have not reported any news from the Navy in months. As of this writing, the talk-polywell forum now has 145,275 registered users - though many accounts are bot accounts. If the Navy gave out any information, people would be reposting it. The Navy, therefore, is keeping quiet.

The Start of a Venture Capital Pitch:

      In order to move forward, we need some kind of vision, an end goal for this technology. This blog would argue, that taking this to a high tech startup with a product, should be our goal. There are many of problems still to be dealt with, but aiming for that end will give a clear path to follow. What information would be needed to convince a venture capitalist to invest, say 20 million dollars into this project? This blog argues that, at present, a VC would be asking many of the same questions a researcher would. Complex questions like: at what temperature would this reactor operate at? Or simple questions like: what is the build price? A pitch would need to make statements like: we need X amount of money for Y equipment to run Z tests. A pitch would need Gantt charts, including deadlines and checkpoints; where if results were good or bad, different courses of action would be taken. A pitch would need statements like: if test A and B go well, we are 85% sure that in 14 months we can have this (picture) built.

The Pitch: Current Patent Protection
     People have argued that investors will need patents. Investors will not even ask about patents, if the idea is crap. The primary Bussard patent was issued May 2, 1989 but had expired by 2006 [14, 15]. Bussard filed again on September 27th 2006 and passed away about a year later. That patent was published in July 14th 2011, thereby making it part of the prior art [16]. It is currently weaving its way inside the US patent office and is listed on the PAIR database as: “on appeal” [17]. It would be interesting if a legal expert could weigh in on the implications, possibilities and scope of the patents; that is outside the focus of this blog.

The Pitch: How could this idea fail?   

   “It doesn't matter how beautiful your theory is, it doesn't matter how smart you are. If it doesn't agree with experiment, it's wrong”. - Richard Feynman

     Any pitch will also contain arguments for and against this reactor working. As far as we know, the main arguments against this working come from Riders’ PhD thesis, his 2005 APS presentation 1995 publication and Bill Nevins’ paper in 1995. This blog has analized and explained of Riders’ publication before. It would be nice to review Bill Nevins’ work as well as Riders’ full thesis. Briefly, here is a summary of Rider’s publication. The reader is encouraged to read “Explaining the counter argument – Part II” for a more detailed explanation of the terminology and concepts.

      Rider assumes the cloud to be quasineutral - meaning that in a local volume there is no net charge. We point out that by definition, the polywell will need more electrons than ions to work, which threatens the quasineutral assumption. Rider would counter by arguing that concentrating charge creates a voltage drop – causing the plasma to swirl around till the charge equilibrates. This would be a plasma instability – a topic we still need to address. We counter by asking the question: what if the polywell ran electron rich, say a ratio of 3:1? Would there be so few ions that the cloud would not be considered quasineutral? Rider assumed the cloud has three parts to it: a core, a mantle and an edge. He assumes that these three parts will remain roughly constant; a best-case-scenario. He argues that this is a weak assumption, because ions will disperse the core. We counter by raising the possibility that the electron cloud has its own magnetic field - an internal resistance to the applied fields. This internal field could pinch off the loss points, deepening the well and improving the machines ability to capture electrons. This may be very good news. Better electron capture would mean a deeper voltage drop, holding the ions more tightly together. This may make it harder for the ions to disperse the core. It also means the ions could be injected with a higher starting energy – improving the odds of fusion.

      In his paper, Rider walks through the following calculations. The first he finds is the fusion rate. He assumes the cloud is quasineutral – an assumption we question above. The expression he found is derived from a general fusion equation – not derived from polywell data. This is shown below for just fusing deuterium, at a uniform density (A). Rider uses this expression to calculate the time to fusion – shown here (B) for just deuterium. Now Rider wants an equation for energy transfer inside the ion cloud. For this, he argues each cloud has a bell curve of energies. Because of this assumption he uses a standard formula, shown in (C) for deuterium only. Imagine we have a cold cloud, which is heating up by energy transfer from the hot cloud, and by fusion reactions. Rider considers the case where all the hot fused ions are replaced by cold ions – and this rate is shown in (D). We would like to point out there are many other heat flows inside the machine, though it makes sense here for Rider to limit himself to focus just on the ions. Rider sets equation (C) equal to equation (D) and integrates over the volume. From this integration he reasons the ion cloud cannot have more than a 5% variation in temperature. This calculation needs polywell data to back it up.

Rider examines a more board case of keeping the ions at two different temperatures. He assumes the ions can be artificially held at two different temperatures and, he wants to see how difficult this is. If you assume the temperatures are very different you can find the average relative velocity on an ion - shown in equation (E). This is an expression from statistics. If this is the case then, rider states all the energy transferred inside the ion cloud will be via collisions. In reality energy transfer could happen several ways: electrons, x-rays and fusion products could transfer energy around the reactor - but they are not considered in this section of Riders’ paper. If collisions alone transfer energy, then this could be adjusted by changing the mean free path. Indeed, the equation Rider uses includes the columbic logarithm, a tool used to find the mean free path in plasma. Rider divides by the fusion rate, and gets equation (F). Rider applies this equation to the P B-11 fusion reaction, and calculates that cooling needs to happen 1.4 times more than the fusion rate to artificially maintain the ions at two different temperatures.

      Next Rider tries to find how fast the ion cloud will go to a bell curve of energies. The time to thermalize is some multiple of the ion-ion collision time. So he needs to find that first. Imagine a test ion. It gets injected into the polywell, towards a mass of ions and electrons in the center. First, let us ignore electron-ion interactions. An electron is about 1,836 thousand times less massive then an ion. When electrons and ions do hit, they can create x-rays. This is a big problem and, Rider will address it later. Rider assumes that the test ion would spend only a short amount of time in the core. This is a valid assumption for Rider, because for his model, the core is ~0.0001% of the total cloud of ions. One argument against this is: if the potential well could better contain the cloud the core should be a larger percentage of the cloud. The core should be denser while the overall cloud would be smaller. But in Riders’ model the ion collision time is given as equation (G). Rider then compares this time to the fusion time and comes up with equation (H). He applies some typical numbers and finds that ion collisions happen 1000 to 100 times faster than the fusion rate. According to these equations a denser cloud - created by the Whiffleball – alone, would not necessarily help. A denser cloud increases the rate of collisions leading to faster thermalization and the rate of fusion, together at the same time. But, it is unclear if these are even the right equations to use – data should clear this up.

     Rider wants to compare the time it takes for the ions to escape the well. This happens through upscattering. There are four cases to consider: the reactor can fuse “big” or “small” ions and the cloud can contain “high” or “low” angular momentum. Ideally, we want to fuse “small” ions - like deuterium – with a plasma cloud with a low angular momentum. To classically estimate this clouds’ angular momentum, we would first find the clouds’ center of mass. We then find how far away each particle is from the center, and what direction and speed it is going, multiply and add all these together. The key point here is: if the cloud is tighter, the angular momentum should be lower. Ideally, we want these electrons moving at a low velocity in a tightly contained magnetic field.

     Rider uses equation (I) as his ion loss rate equation. We are not comfortable with the equation he uses. We insist: we should just build the polywell and measure the loss rate. The loss rate equation has a long history. We spent two weeks researching the origins of this equation. We looked at papers by: Pastukhov (’74), PJ Catto (’84), BenDaniels (’61), and TMX papers from the early 80’s. We focused on the ion loss equations, only. Each theory paper made assumptions about: the well shape, the particle behavior, elastic collisions, the charge on ions, the characteristic collision time and length, the characteristic length of the field, ect… The data papers primarily come from the big magnetic mirror experiments of the early 80’s. With so many variables changing for the polywell, many which also change with time, it is hard to tell if these relations actually apply to the Polywell. That said – the losses from magnetic confinement have been well studied, so perhaps an expert can weigh in here. We should use simple math to forecast. But, forget theory. Build it. Measure the losses.

     Rider goes on to look at x-ray radiation, electron drag and ion injection along with other issues. Readers are encouraged to look at his original papers as well as Nevins work. You can check out “Explaining the counter argument – Part II” for a continued description of what Riders' arguments mean. Any pitch would absolutely need a full summary of these papers and a discussion about what they mean.


The Pitch: The Team

“A great workplace isn’t in a great espresso machine or sushi for lunch, it is in having great collogues.” - Reed Hastings

     At this point, we should care more about the technology and less about the business end. But, if we were to assemble a team to develop the polywell into a product, who would be on it? We argue it should be a partnership of young energy as well as older experience. Here is a list of individuals we considered for the launch of such a company:

1. A plant manager or engineer from the nuclear industry. Someone with experience on the implementation of nuclear power plants.

2. A physicist someone who can research diverse topics, analyze highly complex papers, explain ideas to the team, direct research and train others.

3. A marketer someone who can communicate very complex information and brand the idea to the broad audience. Preferably someone who can use the media of today.

4. A manager someone who can lead the team, set deadlines, mind cash flow and hire people.

5. A manufacturing guy, who knows machining, parts purchasing, engineering of components, someone very experienced and grounded in bringing products to completion. (Possibly Mark Suppes)

6. A sales guy, who can pitch the idea to investors, interface between the customers and the company. Someone who is well networked with the kinds of people needed to get this organization off the ground.

Feel free to add your own interpretation on this list. The folks at talk-polywell have been in discussions about this topic for some time now. Someone has already brought up having a lawyer and an accountant on this list.

The Pitch: Building a Prototype

   Building the basic machine may be the relatively easier step in this whole process. This is one of the advantages of this kind of fusion reactor – at this point, at least – the machine appears relatively easy to construct. It would need: a vacuum chamber, vacuum pumps, ion guns, fuel, electron guns, a neutron counter, a voltage source, a coolant layer for heat capture and the ring structure. It would be great to add diagnostics: such as an x-ray detector and Thompson scattering laser detectors. Fancier tools such as neutron recoil detectors, do exist, but these were custom built for the government research labs and would represent a distraction for any prototype.

     The key for rapid success would be in focusing on the most basic, workable reactor possible. Figure out the fastest way, to the simplest machine, get it working and just churn out devices. That means anticipating as many problems, as earlier as possible. It means standardizing and eliminating variations in design wherever possible. It also means relying as much as possible on established technology. Outsource the maintenance of the ion and electron guns. Have some experienced expert deal with the vacuum chamber and pumps. The goal for the team would be to focus on the “special sauce” – the part of the reactor that is unique. In this case it would be the ring design, coupled with the relative operation of the different components. How strong a potential well are you generating, relative to the ions injected? What is the ideal electron, ion ratio? What are the rates of fusion, x-ray cooling and losses at each mode of operation?

The Pitch: Machine Size:

   In sizing the machine, we have seen bigger and bigger reactors. Mark Suppes and Joe Khackan have both built small (6”) teflon reactors. This was also about the size of Bussards’ WB3 device (‘98 – ’01) [23]. We have also seen one foot devices: WB6 (2005) and WB7 (2008) were both one foot devices. But, recently the planned reactors have gotten bigger. In the last three years, the Iranians and Joel Rogers both simulated reactors over two feet to a side [5, 4]. It is unclear what the size is of the Navy’s WB-8 reactor (11/2010 – present). If the reactor is bigger, it will most likely require a stronger magnetic field to contain material. WB-8 had an eight fold increase in magnetic field strength [17]. These reactors are shown below.

Figure: Different polywell reactors, built, planned or simulated. A) WB-3 developed by Dr. Bussards’ team from 1998 to 2001. This device had a radius of 10 cm or 4 inches [23]. B) A picture of Dr. Khachans’ device developed at the University of Sydney, Australia, in 2009 [6]. This device had a width of 6 cm or 2.3 inches. C) A picture of Mark Suppes device built in Brooklyn New York, in 2011 [24]. D) A schematic of a reactor, patented by Joel Rogers, November 10th 2010. A modification on the polywell design, indications are that this will be over 2 feet a side [4] E) A figure of the polywell design simulated by Iranian researchers in October 2011; this was over two feet to a side [5]. F) A picture of WB-6 developed by Dr. Bussards team in the summer of 2005; this device was about 1 foot a side [23]. G) A picture of WB-8 being operated in 2008 [23].


One could build a small reactor. The advantage here would be a lower price, where all the physics of the machine could be explored. But, you lose the WOW factor. Steve Jobs knew how to capitalize on the WOW factor when selling revolutionary products like the Macintosh. We understand the momentum created by a WOW prototype; in terms of attracting investors, customers and employees. Additionally if the scaling laws are correct, a larger machine would be much closer to net power. Therefore, we argue that a big device should be built.

The Machine: The Design

    The old business adage ‘location, location, location’ – can be substituted in this case for ‘design, design, design’. It is guaranteed that the first prototype will need changes made. If we put in the right design upfront we can save time, money and hassle later. Bussard could not optimize his machine, because he did not know what the ideal reactor looks like. We can do better. We need to apply the principals of six sigma. We need to standardize everywhere – eliminate as many variations as possible. Parts should be interchangeable, modular, and serviceable. Below are some suggested designs.

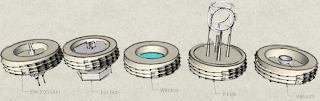
What is pictured is one of six panels 3 feet to a side. The panels fasten together with diagonal screw holes on top and on the outside contain coolant tubes to capture energy. We will probably need more than the nine screws shown to hold vacuum and the coolant tube designs needs rethinking. Each panel has a 15 inch hole in the middle for inserts. These could be windows, X-ray detectors, ion guns, electron guns, the rings themselves, a Fusor or the vacuum pump. Shown below are examples of inserts. The key innovation is that the standardized 15 inch ring can interface with yet unknown tools.  

It is unclear what the best connection for the inserts is. A screw will hold vacuum (shown here), but this means the part will need turning. Ideally we want to slide in an insert and screw it in without turning the whole part. There are of course O-rings which can be used to seal for vacuum. We also considered putting some kind of hinge on the reactor panel to allow the panels to swing out. The power connectors should all be uniform, like the connectors used in home computers. The rings should detach individually, not conduct to the outside and connect the current. The suggestion to solve this problem is by using, slide in, conductive inserts.  

This is a great solution. It allows someone to adjust the distance between the rings on the fly. It makes the rings modular. You can fix one ring individually. It standardizes ring design; making four rings interchangeable. It is simple. It does all this without conducting to the outside vacuum. Certainly there are many more design innovations to add in later. We should undergo at least 3 or 4 more reworks before building this machine.

How To Analyze Reactor:

Goal: Operate Around The Experts

“The experts tell the investor here is the three things that will not work and their mostly right… but it is amazing how many solutions show up when your alternative is death” – Vinod Kholsa

     Rider and Nevins cannot be ignored. They list valid problems with this technology. Discussed above is a summary of some of these issues. They may be correct, and the technology is a dead end – but there is no way to know without credible, honest data. The key is to see if this machine can operate around these problems. Below is a list of possible ideas around these concerns, with some comments on each option. It remains to be seen if these ideas can hold any weight.

1. Tuning to a resonance condition. Based on cross sections, we know that different fusion reactions happen best at different specific energies. Presumably, for that given fuel, the polywell would try and contain enough electrons to hit that voltage. Additionally, the University of Sydney’s work indicates that the amount of electrons “caught” inside the polywell peaks at a specific magnetic field strength. The machine could be tuned. Tuned based on number of electrons and ions, magnetic field strength and injection energy. The machine is also complex. For instance, the more the electrons in the center – the stronger the rejecting inner magnetic field should be. A stronger rejecting field would mean a better contained electron cloud in the middle. With such a complex system, there is a chance the machine has an operational “sweet spot”. A resonance condition, where the rate of fusion spikes.

2. Head on collisions. Unlike the tokamak, all the ions flying into the center. Unlike ICF, escaping ions are sent back into the center. Head on collisions are much more likely. This implies the ion velocity does not need to be as high to get fusion. How could we quantify this advantage, how could we determine what effect this will have?

3. Reflecting the X-rays back in. Is it possible to reflect the X-rays lost back into the plasma? Recycling these losses would seriously reduce energy loss by radiation. X-rays can be reflected using elements with lots of electrons in their K shell, such as gold or lead. Ideally, we would want to do it with cheaper materials. Lead melts at 600 K and gold melts at 1,337 K. We may be able to use these materials in the walls of polywell, if the reactor temperature is low. This is a very, very, exciting idea. An important first question to ask is: what is the ideal reactor temperature?

4. Running Electron Rich. If the center is filled with vast amounts of low energy electrons, creating a large voltage drop, is ion fusion more likely with a handful of ions? Rider made a very strong case that parts of the cloud could not be held at two temperatures. He used the rate of energy transfer from one set of electrons or ions to another set of electrons or ions to make this theoretical argument. We still need data to verify. We know that the hydrogen ion is ~1,836 times more massive than an electron. You cannot really assign a ratio of diameters to the ion and electron (though this blog has in the past) because quantum mechanics pushes the idea that “electrons” to be more like fluffy clouds of potential. An “electron” will fill the space dictated by the charge distributions around it – be it other electrons or nuclei. That said - experiments have measured the radius of the electron to be 1E-22 meters or smaller. This makes a proton 8.5 million times bigger than the electron, or more. Please see the appendix for a more detailed description of this. This means there are two ways one can think about an electron rich polywell. The first is quantum mechanically. The center would be a giant fluffy, pulsating cloud of potentiality. Where the electrons would just fill the space provided by the net magnetic containment field. In this cloud, high velocity, big ions can fly in and hit one another. The second is classically. The electrons and ions have a shape. The electrons are about the size of atmospheric dust while the ions are about the size of large (3”) marbles. They are held together in a bed sheet – to represent the potential well. A picture of these two analogies is shown below. The ions are released from the sides of the bed sheet and fall into the center – or injected by ion guns and fall into the center. The point is the ions are so much more massive and larger than the electrons.

5. Exploiting the ion’s charge. Accelerating ions using a voltage means the machine can take advantage of ions with a high charge on them. For example: An ion with a charge of five, sees five times more acceleration with the same electron cloud in the center. This means we get a huge increase in the velocity of the ion with the same electron cloud. A subtler point is: we could use two sets of ions, to get two different accelerations with the same cloud. Is there any way that this could be exploited to help the fusion rates?


6. Games with Ion Injection. Can you play some game with ion injection, to fuse at a lower cloud temperature? Ion injection offers you control over starting the ions out at a high enough velocity. This seems very doubtful; during normal operation where the ion to electron ratio is closer to 1:1. The cloud has more ions in this case; as soon as the ions enter the cloud it can hit another ion and not fuse. In this case the sum energy contained between both ions is basically spilt between the then. Rider argued, that this will rapid cool off the population of ions inside the machine. One way to test this hypothesis is to calculate the Mean Free Path of the ion cloud, at different densities. More generally, Rider argued strongly that ion injection was going to be a problem. However, Rider may not have considered how the Whiffle ball affected this. With better electron containment, a deeper well can be formed, allowing for deeper, higher velocity ions to be injected. But, this may not be a “game changing” effect.

7. Direct Conversion Drives Machine Efficiency up. Theoretically, direct conversion should recover energy with a higher efficiency then Lawson’s 33%. We discuss the Lawson criteria below. Direct conversion is an idea where the fusion products – naked nuclei – are slowed down in a voltage field. When they reach the metal surface they draw electrons at that high voltage. The idea was conceived by Richard Post in the 1980’s. Some basic tests were done exploring the technology [22] – but the method is hardly mature. Besides it is not clear how a voltage fields around the reactor can co-exist with the voltage fields already needed to run the machine. Someone really needs to explore the idea of direct conversion and the polywell as it is currently conceived.


Physics Analysis: Using Dimensionless Numbers: 
     Experimentation can suck. Take some experiment: like dropping a rubber ball. You want to figure out what changes, how high the ball bounces back. That might sound easy, but it is not. Consider all the variables in that experiment: variables such as the balls’ velocity, the air viscosity, the elasticity of the rubber and the hardness of the floor. Now imagine you wanted to test dropping the ball, you could vary each variable on this list separately; like turning seven nobs, independently. To change volume you could drop 15 balls, each a different size and graph how high they bounce back. This is silly. Finding what controls bounce height would take forever. The experiment would need to be simplified. It was recognized then, that these variables were related. These variables could be combined – into dimensionless groups. In the case of the rubber ball, one the dimensionless group of interest was the drag coefficient.

These dimensionless groups simplify the variable space. Instead of seven knobs to turn, you could now turn only one or two. Many systems have dimensionless numbers: from plasma systems to physical systems to heat conduction. The polywell may have its own dimensionless numbers. The man who first devised the method of finding dimensionless numbers was Lord Rayleigh, in England, in the 19th century. There are two obvious dimensionless numbers we already know about. These are shown below.  

Bussard talked extensively about the first group, the beta ratio in his work. It is a common number used in magnetically confined plasma. It is a ratio of the plasma pressure (on top) and the magnetic field containing it (on the bottom). The second number is an obvious choice: a ratio of the number electrons to the number of ions in the machine. The goal would be to vary the values of these numbers to see how much fusion we get from the machine. There may yet be other dimensionless numbers in the polywell. Below we attempt to tease out others.

Rayleigh's method of Dimensional Analysis

    Finding dimensionless groups in a new system can be tricky. First, you need to gather all the independent variables. Pick the relevant ones; the ones that will likely affect the outcome of the experiment. Next you need to identify what you are trying to measure; name that variable as a dependent. Once that is done there is a nice formula which predicts how many dimensionless groups you expect to find. This is the Buckingham-pi theorem [11, 12]. Edgar Buckingham created this theorem to predict how many groups there were in a given experiment. He was a physicist working for the US government during the first half of the 20th century.

This method has been used in the past to simplify complex problems. Applying this method to a complex system like the polywell should help us simplify experimentation. This is not an easy task – and people are welcome to critique how well we did. The goal is to reduce the variables you need to explore when operating this machine. We hope to also find established numbers that may apply to this system.


Rayleigh's method Applied To the confinement Field

      For example, let’s apply this method to just the magnetic confinement field. Here is a list of all the independent variables I expect will affect the actual magnetic containment field, the machine makes.

1. The number of rings [dimensionless]
2. The ring width - [meters]
3. The circumference of the rings - [meters]
4. The minimum spacing between each ring - [meters]
5. The magnetic field each ring creates per ring section - [tesla/meter – (kilogram / meter * amp * second^2)]
6. The magnetic field of the electron cloud pressing back against the ring field - [tesla – (kilogram / amp * second^2)]

That is a list of all the independent variables; we would expect to be important. Variables 1 through 4 deal with the geometry of the system. Variables 5 and 6 deal with the magnetic field strength. There is also a 7th variable; the dependent one, the actual magnetic containment field we generate. Now according to Rayleigh's method if one variable depends on 6 other independent variables, then a function can be written to relate these, this is shown below [10].

This function is essentially, a mathematical representation of our experiment. We are testing, to figure out how changing six of these factors, affects the 7th factor. This is a really important concept to grasp. Think about it. If, in reality, these six factors are the independent reasons for the 7th factor being what it is, then they are related in reality. If they are related in reality, then they can be related mathematically. This is an important and profound concept to understand.


Applying Buckingham-Pi:

    We do not know what this function is, nor do we need to know it, for our current purposes. Let us assume this function exists. Now, let us apply the Buckingham-pi theorem to this function. You should include the variable you seeking; so there are 7 variables. There are also 4 dimensions: meters, amps, kilograms and seconds.

This theorem predicts how many dimensionless groups you should find in Rayleigh's relationship. It cannot tell you which of these groups are physically meaningful. In more complex problems, you would now use matrix mathematics to find these groups. In fact, it was assuming that these factors could be entered into a matrix which led Buckingham to create the formula in the first place [11, 12]. The wikipedia article steps through two examples of applying matrix algebra to find the dimensionless numbers. This is unneeded here, as it is easy to see all the dimensionless groups one could make from our variables. These are included below.

As we can see, there are 4 dimensionless groups listed here, where as the formula only predicted 3. Someone has pointed out that dimensionless groups, 4 - 6 are not independent of one another, which may account for this difference. If a more experienced expert could weigh in on this unexpected result, we would appreciate it. There is also the possibility of not including the number of rings in group 3, since this variable has no dimensions. However if a machine, for example, had 48 rings this number would clearly contain needed information – so it was included. Some of these dimensionless groups are not physically meaningful. For example, what use would the ratio of the ring width over the ring spacing, have? It is clear that there is a dimensionless group to describe the ratio of the externally applied magnetic field to the magnetic field generated by the electron cloud. This is not a surprise, nor is this new. There are certainly dimensionless numbers known today, which are the ratio of two magnetic fields.

     You could call it the Whiffleball Number. Someone would need to figure out how to use such a number effectively. How can we measure the magnetic field created by the electron cloud? There are commercially available gauss meters for measuring magnetic fields, but how could one focus on only the field of interest? If viable, simulations may be the best method for testing this dimensionless number and simulations themselves can be tricky. The idea would be to vary this number from say, 0.01 to 100 and see what effect it has on the fusion rate.

Applying Method to Voltage

      Picking the variables is the hardest part about applying this method to experimentation. You need to pick variables which directly affect the phenomenon you are interested in and you need to pick variables that are independent of one another. Below are variables related to the potential well and the ion injection voltage.

1. The voltage of the ion source – Voltage – (kilogram * meter^2/ second^2 * Amp)]
2. The net charge in the center of the device – Amps
3. The distance from the gun to the center – [meters]
4. The permittivity of free space –[(Amp^2 * Second^4)/(Meters^3 * kilograms)]
5. Pi – [dimensionless]

These variables predict that there is 1 dimensionless group that can be formed. This group is shown below. It is the ratio of the voltage created by the charge in the center of the device and the voltage of the ion beam injected into the center. The group comes out of the electric potential equation for a point charge.

This group may actually be very useful; imagine an experiment where we vary the voltage of the ion source against the voltage inside the well. We could run through dimensionless quantities of 0.01 to 100 and see what this does to our fusion rate.   Edit: Several people have pointed out that ion injection, may not have a voltage - in which case this number would not apply.  You can see a detailed discussion here:  http://www.talk-polywell.org/bb/viewtopic.php?p=79243&sid=bbbfc496404fd5d406864f5ab8e34f9a



Analysis II: Engineering analysis, mass and energy balances

   Traditional engineers do not use dimensionless numbers to analyze systems. They let the physicists do that. Another approach to analyzing these machines is to do an electron, ion and energy balance across the machine. The goal would be to figure out the rates. What is the rate of ion loss? What is the rate of electron loss? Try and find equations for each rate and from that ask questions about operating the polywell. We can start by looking at the number of ions and electrons inside the polywell. To do a mass balance we need to know the number injected, held and lost.

Analysis III: Science analysis, applying the Lawson criteria to the polywell

     John Lawson was 33 when he made one of his most important contributions to fusion research; the Lawson criteria. This simple concept has been the benchmark that we test all fusion ideas against. Simply put: in order to fuse plasma, the cloud must produce more energy than it takes to fuse it. Lawson assumed that to get a viable reactor, you need to heat up the plasma cloud. He also assumed once fused, the hot material leaves. As the temperature rises, the cross section – the measure of the fusibility of A and B – generally rises. Rising temperature also means the average velocity of the plasma is rising. This means the plasma is more like to fuse. Rising temperature also means the plasma loses energy. Hot plasma mainly loses energy through conduction and radiation. So this pits two rates against one another: the rate of energy loss and rate of energy produced by fusion. Lawson argued you needed to reach a critical temperature. A temperature where energy produced overtook energy lost. This is shown graphically below.

Figure: A hypothetical sketch, laying out competing rates of energy generation and energy losses in a hot plasma fusion reactor. These rates were discussed by JD Lawson in his 1957 paper; but what is drawn here is merely a graphic. Lawson assumed that the reactor relies on heating up the plasma, and that the fusion products leave the reactor.

He estimated that this temperature was about 150 million degrees for deuterium-deuterium fusion and 30 million degrees for deuterium-tritium fusion. Lawson wanted a simple math expression which would tell him if a reactor would produce power. We adapted the expression from his paper and included it below.

For the machine to make electricity, the above equation must be met. Lawson reasoned that the highest machine efficiency could get was 33%. If the machine efficiency is only 33%, then the energy released by the reactor has to be twice the energy fed in.

     The Lawson criterion has been around for 55 years, so long that many people have not read the original paper. It naturally allows only two paths to fusion energy. Either contain hot plasma at high pressures for a short time or contain plasma at low pressures for a long time. This leads to two methods for fusion with hot plasma: compress plasma with laser beams (Pressures in the gigabars for ~10 nanoseconds) or race hot plasma around a ring for a long time in tokamaks (Pressures of ~1 atmosphere for ~300 seconds).

      There are two methods; that is it. But then, how does the Fusor fit into this picture? The Fusor is a proven path to fusion; it fuses material with a relatively cold, uncompressed cloud of ions (pressures ~0.1 – 50 millitorr) [1]. It should be mentioned here that Farnsworth built the Fusor roughly ten years after Lawson published his now famous paper. Anytime you read about a high school student doing fusion at their home - with cheap equipment - they are using a fusor. At first glance, this seems to fly in the face of the Lawson criterion. But, researchers will argue: fusors will never make net power and you need to meet the Lawson criterion to make net power. This is true we do need to make net power. It is estimated that in a typical Fusor only 1 in every 100,000 ions injected, actually fuse [2].

      Lawson imagined a reactor with hot confined plasma which would lose most of its energy through conduction and radiation. Fusors do not have hot or, highly confined plasma. They operate on the relatively low end of the temperature scale. They do suffer from both conduction and radiation losses. The worst losses coming from conduction: the ions and their associated energy are being conducted through the cages. The whole idea of the polywell is too seriously reduce this problem. The polywell design evolved from the fusor to eliminate conduction losses. This machine attempts to do it three ways: by eliminating the metal cages which conduct out the ions, by insulating the rings as a conduction path and by using the diamagnetism of the cloud itself to better contain the electrons and by extension the ions.

      This leaves energy radiation as the primary hurdle for the polywell. This is why so much of Todd Riders and Nevins work focused on Bremsstrahlung (or x-ray) cooling and plasma structure. A plasma cloud can leak much of its energy out through X-rays; but leakage depends on the structure, temperature, density and composition of the plasma cloud. The actual structure (if any) of the plasma inside the polywell is still an open question. Wither a virtual anode forms remains to be proven and how this might affect x-ray production is unknown.

      If the Fusor can fuse on the relatively cold end of the plasma temperature, why can’t the polywell? Rider makes a very strong case you cannot do this, you cannot have two temperatures inside the reactor. Rider argued that the temperatures could be at most 5% different from one another [3]. Someone should build a machine and test this. If there was some way to fuse hot ions with cold electrons it would make the Lawson criterion less relevant. Cold plasma loses much less energy by radiation, then hot plasma. The hope would be that energy losses would be lowered so much, that we could actually get net power. Cold plasma is easier to work with, eliminating many engineering and cost hurdles. Ideally, you want a cloud of cold electrons attracting high velocity ions. But, we do not know if this is possible.

      If the cloud must be all at one temperature and that temperature must be hot, then the reactor will generate lots of x-rays. At this point, the success of the reactor becomes highly questionable. Only experimentation can determine if there is a chance any of the ideas mentioned above can change this. One path which looks promising is trying to reflect the x-rays back into the center.

Future Work: Diagnostics and Plasma Instabilities

     There are two other topics we planned to address, but could not find the time for. These are diagnostics and plasma instabilities. On the subject of diagnostics we planned to make a list of all the techniques that may work to study plasma inside the polywell. We considered shadowgraphy; this will probably not be helpful. We considered x-ray radiography; which will probably also be a dead end. We wanted to get more information about Thompson scattering and magnetic recoil spectrometry. Ideally, we want a tool which will tell us the density of the plasma over time. We want a movie showing the clouds of plasma: where they are dense, where they turn around and how fast they are moving. These “movies” could be taken during some useful tests. What if during operation electron and ion injection were suddenly cut off? How long would it take for the ion and electron clouds to dissipate and where would the major losses be? What if during operation the magnetic field was cut in half? Would the plasma cloud double in volume? Consider though, a startup may skip diagnostics work.

      One the subject of plasma instabilities, we wanted to make a list of all the relevant plasma instabilities applicable to this technology. A quick count on wikipedia gives over 50 known plasma instabilities [26]. Someone needs to go through and figure out which of these instabilities is most likely a problem for the polywell. We need to add this information into our designs upfront to save time and money. Much of the work with instabilities can be traced to the “pope” of plasma physics Marshall Rosenbluth.

Appendix A: The ratio of ion to electron diameter:

     In classical physics, the electron has a radius: 2.8179 E-15 meters. This is known as the “classical electron radius”. But this does not take into account quantum field theory. Quantum field theory states that an electron will - kind of - fill the space provided to it. Thus, the “classical electron radius” is no longer considered the actual size of an electron. We know that a proton has a radius of ~ 8.6E-16 meters. So if we take a simple ratio of the two we get that an electron is ~3.3 bigger than an ion.

     But, we also have an experimental measurement of a single electron. This was done by trapping an electron inside a magnetic field – also known as a penning trap. These devices are similar to polywells in that they trap charged particles in magnetic fields. That shows that the radius of the electron is 1E-22 meters or smaller. Take a simple ratio and we see the ion is ~8.5 million times bigger than the electron, or more. [18 – 21] We wanted to develop an analogy for this, so we needed to find particles with the same relative sizes. We settles on atmospheric dust (1E-9 meters diameter) and large marbles (0.007 meters in diameter). We imagined these particles held in a bed sheet, representing the potential well. The marbles were release on the sides, and fell towards the middle, hitting one another and fusing. These calculations are shown below.

 

Works Cited:

1. McGuire, Thomas. Improved Lifetimes and Synchronization Behavior in Multi-grid Inertial Electrostatic Confinement Fusion Devices. Diss. Massachusetts Institute of Technology, 2011. Print.

2. Dietrich, Carl. Improving Particle Confinement in Inertial Electrostatic Fusion for Spacecraft Power and Propulsion. Diss. Massachusetts Institute of Technology, 2007. Print. page 13.

3. Rider, Todd H. "A General Critique of Inertial-electrostatic Confinement Fusion Systems." Physics of Plasmas 6.2 (1995): 1853-872. Print. An Interview with Thomas Ligon.

4. Rogers, Joel G. "A “Polywell” P+11B Power Reactor." The School of Physics. The University of Sydney. Web. .Joe Khackans newest paper, December 2011.

5. Kazemyzade, F., H. Mahdipoor, A. Bagheri, S. Khademzade, E. Hajiebrahimi, Z. Gheisari, A. Sadighzadeh, and V. Damideh. "Dependence of Potential Well Depth on the Magnetic Field Intensity in a Polywell Reactor." Journal of Fusion Energy (2011). Web.

6. Carr, Matthew. "Low Beta Confinement in a Polywell Modeled with Conventional Point Cusp Theories." The Physics of Plasmas 18 (2011): 112501-12501-9. Print.

7. Damideh, V., and A. Sadighzadeh. "Experimental Study of the Iranian Inertial Electrostatic Confinement Fusion Device as a Continuous Neutron Generator." Journal of Fusion Energy (2011). Web.

8. Fitzpatrick, Richard. "Particle-in-cell Codes." Home Page for Richard Fitzpatrick. The University of Texas at Austin, 29 Mar. 2006. Web. 02 Feb. 2012. .

9. Damideh, V. "View Topic - New Polywell Reactor Article in Journal of Fusion Energy." Talk-Polywell.org. Talk-Polywell, 21 Oct. 2011. Web. 02 Jan. 2012. .

10. "Rayleigh's Method of Dimensional Analysis." Wikipedia. The Wikipedia Foundation, 15 Mar. 2011. Web. 12 Jan. 2012. .

11. "Buckingham π Theorem." Wikipedia, the Free Encyclopedia. The Wikipedia Foundation, 31 Jan. 2012. Web. 02 Feb. 2012. .

12. Buckingham, Edgar. "On Physically Similar Systems; Illustrations of the Use of Dimensional Equations." Physical Review 4.4 (1914): 345-76. Print.

13. "Term of Patent in the United States." Wikipedia, the Free Encyclopedia. The Wikipedia Foundation, 13 Jan. 2012. Web. 04 Feb. 2012. .

14. Bussard, Robert W. Method and Apparatus for Controlling Charged Particles. US, assignee. Patent 4,826,646. 2 May 1989. Print.

15. Bussard, Robert W. Method and Apparatus for Controlling Charged Particles. Ricardo J Palabrica, assignee. Patent Application 2011/0170647. 9 Sept. 2006. Print.

16. Patent Application Information Retrieval. United States Patent & Trademark Office, 25 Jan. 2012. Web. 25 Jan. 2012. .

17. "The Polywell." Wikipedia. The Wikipedia Foundation. Web. 28 Dec. 2011. .

18. "Proton." Wikipedia, the Free Encyclopedia. The Wikipedia Foundation, 28 Jan. 2012. Web. 02 Feb. 2012. .

19. "Electron." Wikipedia, the Free Encyclopedia. The Wikipedia Foundation, 1 Feb. 2012. Web. 02 Feb. 2012. .

20. "Penning Trap." Wikipedia, the Free Encyclopedia. The Wikipedia Foundation, 8 Nov. 2011. Web. 02 Feb. 2012. .

21. "Classical Electron Radius." Wikipedia, the Free Encyclopedia. The Wikipedia Foundation, 29 Oct. 2011. Web. 02 Feb. 2012. .

22. Barr, William L., R. W. Moir, and G. W. Hamilton. "Experimental Results from a Beam Direct Converter at 100 Kv." Journal of Fusion Energy 2 (1981): 131-43. Print.

23. Emc2 Fusion Development Corporation. Web. 29 Jan. 2012. .The Advent of Clean Nuclear Fusion: Superperformance Space Power and Propulsion

24. Suppes, Mark. Prometheus Fusion Perfection. Web. 02 Feb. 2012. .

25. Lindl J. D. 1998 Inertial confinement fusion: the quest for ignition and energy gain using indirect drive (New York Springer) 61-82 chapter 6.

26. Plasma Stability. Wikipedia. Wikimedia Foundation, 29 Dec. 2011. Web. 20 Feb. 2012. .